Inscribed Square

Where there is matter, there is geometry. — Johannes Kepler

1.7 Inscribed Square
Level Information
Instruction:	Inscribe a square in the circle. One vertex of the square is given.
Goal:	6L 7E
Available Tools:
Location Information
Pack:	Alpha
Previous Level:	1.6 Circle Center
Next Level:	2.1 Angle Bisector

Solutions

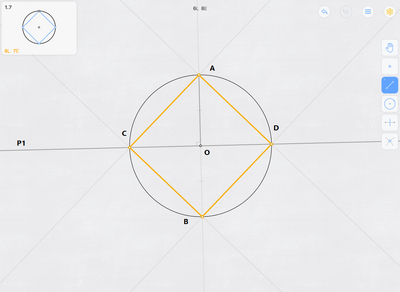
Let O be the center of the circle and A the vertex.

6L Solution

1. Construct line OA, intersecting the circle at point B.
2. Construct the perpendicular bisector of AB, intersecting the circle at points C and D.
3. Construct line AC.
4. Construct line BC.
5. Construct line BD.
6. Construct line AD.

---

7E Solution

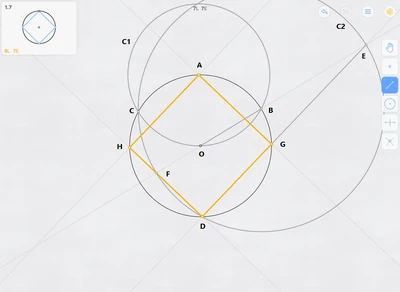
1. Construct the circle with center A and radius OA, intersecting circle O at points B and C.
2. Construct the circle with center B and radius BC, intersecting circle O at D.
3. Construct line OB, intersecting circle B at points E and F.
4. Construct line ED, intersecting circle O at point G.
5. Construct line AG.
6. Construct line DF, intersecting circle O at point H.
7. Construct line AH.

Explanation

Solution 6L is easy as the inscribed square's center is the same as the circle's center, so you can find the vertex opposite to A as its diametrical opposite. That diameter is also a diagonal of the square, so by constructing its perpendicular bisector and second diagonal of the square, you can find the two remaining vertices and just need to trace the whole square.

Solution 7E is trickier. By construction, ABOC is a rhombus, and ABO and ACO are equilateral triangles as all their sides are equal. Therefore, AO and BC (the rhombus's diagonals) are perpendicular bisectors to each other, and angle BOC is 120°.

By construction as well, BCD is an isosceles triangle as BC=BD, and since angle ∠BDC is the inscribed angle that subtends the same arc as the central angle ∠BOC, ∠BDC=120°/2=60°. Therefore, BCD is also an equilateral triangle and AO is one of its bisectors and passes through D, making A, O and D collinear and A and D diametrical opposites on circle O.

Constructing line OB gives you EF, a diameter of circle B, and as such, EDF is a right triangle. And since AD is a diameter of circle O, AGD and AHD are right triangles as well. So, AGDH has three right angles and is therefore a rectangle. In fact, you can construct any diameter EF of circle B (that doesn't pass through point O) and similarly prove that the resulting AGDH is a rectangle.

Now, the fact that the diameter EF passes through point O allows you to determine several angles, for example angle ∠ADG.

∠ADG=∠ADB+∠BDG

∠ADB is known since the triangle BDC is equilateral and AD is one of its bisectors, so ∠ADB=60°/2=30°.

∠BDG=∠BEG since the triangle BED is isosceles. Also ∠BEG is the inscribed angle that subtends the same arc as the central angle ∠FBD in circle B, so ∠BEG=∠FBD/2. Also, in circle O, ∠FBD is the inscribed angle that subtends the same arc as the central angle ∠FOD, so ∠FBD=∠FOD/2. ∠FOD itself is known as it's the opposite angle of ∠AOB and is therefore 60° as AOB is equilateral. So ∠BDG=∠BEG=∠FBD/2=∠FOD/4=60°/4=15°

So ∠ADG=∠ADB+∠BDG=30°+15°=45°, which makes triangle AGD right and isosceles. Therefore, the two adjacent sides AG and GD of the rectangle AGDH are equal, which makes AGDH a square.

List of Levels

Alpha Angle of 60° • Perpendicular Bisector • Midpoint • Circle in Square • Rhombus in Rectangle • Circle Center • Inscribed Square Beta Angle Bisector • Intersection of Angle Bisectors • Angle of 30° • Double Angle • Cut Rectangle • Drop a Perpendicular • Erect a Perpendicular • Tangent to Circle at Point • Circle Tangent to Line • Circle in Rhombus Gamma Chord Midpoint • Triangle by Angle and Orthocenter • Intersection of Perpendicular Bisectors • Three equal segments - 1 • Circle through Point Tangent to Line • Midpoints of Trapezoid Bases • Angle of 45° • Lozenge • Center of Quadrilateral Delta Double Segment • Angle of 60° - 2 • Circumscribed Equilateral Triangle • Equilateral Triangle in Circle • Cut Two Rectangles • Square Root of 2 • Square Root of 3 • Angle of 15° • Square by Opposite Midpoints • Square by Adjacent Midpoints • Square by Two Vertices Epsilon Parallel Line • Parallelogram by Three Vertices • Line Equidistant from Two Points - 1 • Line Equidistant from Two Points - 2 • Hash • Shift Angle • Line Equidistant from Two Lines • Circumscribed Square • Square in Square • Circle Tangent to Square Side • Regular Hexagon Zeta Point Reflection • Reflection • Copy Segment • Given Angle Bisector • Non-collapsing Compass • Translate Segment • Triangle by Three Sides • Parallelogram • Nine Point Circle • Symmetry of Four Lines • Parallelogram by Three Midpoints Eta Sum of Areas of Squares • Annulus • Angle of 75° • Line Equidistant from Three Points • Heron's Problem • Circumscribed Circle • Inscribed Circle • Circle Tangent to Three Lines • Segment by Midpoint • Angle Isosceles • Excircle Theta Perimeter Bisector • Angle 54° Trisection • Interior Angles • Regular Octagon • Triangle Cleaver • Torricelli Point • Circle Equidistant from Four Points • Octagon from Square • Egyptian Triangle by Side of Length 4 • Chord Parallel to Segment Iota Minimum Perimeter - 1 • Third Proportional • Harmonic Mean of Trapezoid Bases • Drop a Perpendicular* • Midpoint* • Trisection by Trapezoid Diagonals • Minimum Perimeter - 2 • Harmonic Mean of Segments • Triangle by Angle and Centroid • Triangle Mid-Segment Kappa Tangent of Circle • Outer Tangent • Inner Tangent • Rotation 90° • Rotation 60° • Segment Trisection • Segment Trisection* • Chord Trisection • Three Circles - 1 • Secant Bisection • Three Circles - 2 • Center of Rotation Lambda Fourth Proportional • Geometric Mean of Segments • Golden Section • Angle of 54° • Third Parallel Line • Circle in Angle • Geometric Mean of Trapezoid Bases • Regular Pentagon • Point Farthest from Angle Sides • Ratio 1 to 5 Mu Triangle by Midpoints • Triangle by Side and Centroid • Triangle by Altitude Base Points • Triangle by Tangent Points • Triangle by Excenters • Equilateral Triangle by Centroid and Two Points • Right Triangle by Two Points on Legs • Hypotenuse and Altitude • Hypotenuse and Leg • Isosceles Triangle by Tangent Points Nu Circle Tangent to Line and Circle • Equilateral Triangle - 2 • Equilateral Triangle on Concentric Circles • Square in Triangle • Point Equidistant from Side of Angle and Point • Circle Through Two Points and Tangent to Line • Inscribed Square - 2 • Line Reflection • Square by Four Points Xi Rhombus in Triangle • Circle Tangent to Two Circles • Triangle by Tangent Point on Hypotenuse • Parallelogram on Four Lines • Arbelos Omicron Midpoint* • Copy Circle • Line-Circle Intersection • Three Equal Segments • Tangent to Circle* • Napoleon's Problem • Drop a Perpendicular** • Line-Circle Intersection* • Circle with Center on Line • Angle of 3° • Mickey Mouse Tutorials Equilateral Triangle • Intersect Tool • Perpendicular Bisector • Move Tool • Angle Bisector • Perpendicular • Parallel Line • Compass