No edit summary Tag: Source edit |
Tag: Visual edit |
||
| (3 intermediate revisions by one other user not shown) | |||
| Line 15: | Line 15: | ||
*Intersect |
*Intersect |
||
| − | + | <u>Pack:</u> [[Beta]] |
|
| − | + | <u>Previous level:</u> [[2.6]] |
|
| + | |||
| + | <u>Next level:</u> [[2.8]] |
||
==1L solution== |
==1L solution== |
||
| Line 25: | Line 27: | ||
==3E solution== |
==3E solution== |
||
| + | [[File:2-7-Erect-Perpendicular.jpg|thumb]] |
||
Let O be the point. |
Let O be the point. |
||
| Line 35: | Line 38: | ||
Solution 3E makes use of Thales's theorem. You are constructing the inscribed triangle OBC with its side BC a diameter of the circle, which makes OBC a right triangle with ∠BOC=90°. |
Solution 3E makes use of Thales's theorem. You are constructing the inscribed triangle OBC with its side BC a diameter of the circle, which makes OBC a right triangle with ∠BOC=90°. |
||
| + | [[Category:Level]] |
||
Revision as of 02:33, 28 February 2022
Instruction: Erect a perpendicular from the point on the line.
Goal: 1L 3E
Available tools:
- Move
- Point
- Line
- Circle
- Perpendicular Bisector
- Angle Bisector
- Intersect
Pack: Beta
Previous level: 2.6
Next level: 2.8
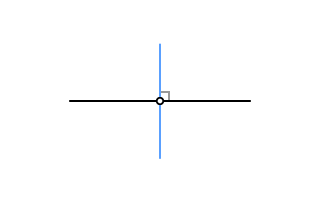
1L solution
Let O be the point, and A and B two arbitrary points on the line so that O is between them.
- Construct the angle bisector of ∠AOB
3E solution
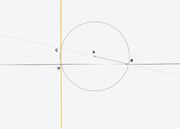
Let O be the point.
- Construct a circle with an arbitrary center A not on the line and radius OA, intersecting the line at B
- Construct line AB, intersecting circle A at C
- Construct line OC
Explanation
Solution 1L is simple as a line is an angle of 180°, so its angle bisector will divide it into two angles of 90° and will therefore be perpendicular to it. Just have the vertex of the 180° angle be point O.
Solution 3E makes use of Thales's theorem. You are constructing the inscribed triangle OBC with its side BC a diameter of the circle, which makes OBC a right triangle with ∠BOC=90°.